[알고리즘] 너비 우선 탐색 (BFS)

들어가기

먼저 너비 우선 탐색(BFS)에 대해서 배워보기 전에 그래프란 무엇인지에 대해서 간략하게나마 알 필요가 있다.

그래프란?

→ 노드(vertex)와 간선(edge)을 가지고 만들어지는 비선형 데이터 구조를 말한다.

그래프는 주로 데이터 간의 관계를 표현할 때 사용된다.

그래프에서 탐색 경로를 찾는 방법은 크게 총 2가지가 있다.

더 이상 탐색할 노드가 없을 때까지 계속 타고 들어간다. 타고 들어가다가 더 이상 탐색할 노드가 존재하지 않으면 백트레킹을 통해 최근 방문했던 노드로 되돌아간다. 그 후 그 노드로부터 가지 않은 노드를 방문한다. 이 과정을 그래프에서 모든 노드를 탐색할 때까지 반복한다. (깊이 우선 탐색 DFS)
현재 위치에서 가장 가까운 노드부터 모두 방문하고 그 이후 다음 노드로 넘어간다. 넘어간 노드로부터 또 가장 가까운 노드를 탐색해 방문한다. 이 과정을 그래프에서 모든 노드를 탐색할 때까지 반복한다. (너비 우선 탐색 BFS)

이번 게시글에서는 너비 우선 탐색(Breadth-First-Search)에 대해 알아보려한다.

📌 깊이 우선 탐색 (DFS) 과정이 궁금하다면?

https://kimhyeongi.tistory.com/97

[알고리즘] 깊이 우선 탐색 (DFS)

들어가기먼저 그래프에서의 탐색 방법들에 대해서 배워보기 전에 그래프란 무엇인지에 대해서 간략하게나마 알 필요가 있다. 그래프란?→ 노드(vertex)와 간선(edge)을 가지고 만들어지는 비선형

kimhyeongi.tistory.com

너비 우선 탐색 (BFS)

BFS에서의 B를 나타내는 Breadth는 "폭"을 의미한다. 즉, 말 그대로 해석하면 폭을 기준으로 가장 먼저 접근하여 탐색하는 방법이라는 뜻이다. 정리해서, BFS는 시작 노드와 거리가 가장 가까운 노드를 우선하여 방문하는 방식으로, DFS처럼 깊게 세로로 들어가는 느낌이 아니라 가로로 넓게 방문하면서 아래로 내려가는 느낌의 탐색 알고리즘이다.

여기서 주의해야 할 점은, 여기서 말하는 '거리'라는 것이 흔히 가중치의 합으로 오해할 수 있지만 시작 노드와 목표 노드까지의 차수를 의미한다는 것이다. 간단하게 과정을 나타내면 시작 노드를 정한 후, 시작 노드를 Queue에 push함과 동시에 방문 처리를 한다. BFS는 재귀 함수를 사용하는 DFS와 다르게 Queue를 사용하는데, Queue 안에 있는 노드는 이미 방문을 한 번 했으나, 해당 노드와 인접한 노드는 아직 방문을 하지 않은 상태라고 생각하면 될 것 같다. 이 과정을 Queue 안에 노드가 더 이상 없을 때까지 반복하면 된다.

BFS 과정 순차적으로 정리하기

과정을 시작하기 전에 시작 노드를 정하고 시작노드를 큐에 먼저 푸시하는 단계가 필요하다.

큐가 비었는지 먼저 확인한다. 큐가 비어있다면 가능한 모든 노드들을 방문했다는 의미이므로 탐색을 종료한다.

01 단계에서 큐가 비어있지 않다면, 큐에서 노드를 팝한다.

팝한 노드와 인접한 노드들을 확인하고 그 중에서 아직 방문하지 않은 노드들이 있다면 그 노드들을 큐에 푸시한 후, 방문 처리한다.

❗️ 팝한 노드와 직접적으로 연결된 인접한 노드들을 모두 방문할 수 있어야 한다.

❗️ 이미 방문했던 노드인지를 확인할 수 있어야 한다.

BFS는 먼저 방문했던 노드들을 먼저 접근하는 방식으로 되어있기 때문에 FIFO(First In, First Out) 구조로 되어있는 Queue를 활용한다.

BFS 핵심 알아보기

BFS는 먼저 방문했던 노드일수록 나중에 다시 접근하는 방식이 아니라, 다시 다음 라인으로 갔을 때 제일 먼저 접근하는 방식이라는 걸 기억하자. DFS는 Stack이 아닌 Queue(FIFO 구조)로 구현하는 점을 잊지 말아야 한다.

BFS의 과정을 세부적으로 따라가보자

노드 상태 처리 (색상)

White : 아직 방문하지 않은 노드
Skyblue : 이미 방문처리는 했으나, 인접노드는 아직 방문하지 않은 노드
Grey : 방문처리 되었고, 인접노드들도 모두 방문처리된 노드

Step 1

시작노드로 설정한 A를 큐에 푸시하고 방문처리한다(하늘색 처리).

Step 2

큐가 비어있는지 확인하고 큐가 비어있지 않다면, A를 팝한 후 A와 인접노드인 D, E에 접근한다. (동시에 접근하는 것처럼 보이지만 실제로는 Queue에 들어오는 순서대로 방문하는 것으로 이해하면 될 것 같다)

D, E 노드들은 아직 방문하지 않았으므로 방문처리해주고(하늘색 처리) A노드는 방문처리됐고, 인접 노드들 역시 모두 방문처리되었으므로 회색으로 처리해준다.

Step 3

큐가 비어있는지 확인하고 큐가 비어있지 않다면, 큐의 가장 가장자리에 위치해있는 D를 팝해준 후 D와 인접한 노드인 B, C에 접근한다.

아직 B, C 노드 모두 방문한 적 없으므로 방문처리하고 D노드는 더이상 접근할 수 있는 인접노드가 없으므로 회색 처리해준다.

Step 4

큐를 확인한 후, 큐의 가장자리에 위치한 E 노드를 팝하고 E의 인접 노드들인 A, D노드에 접근한다. 하지만 A와 D 노드는 모두 이미 방문 처리되었기 때문에 따로 아무 활동도 하지 않는다. E 노드는 방문처리되었고, 인접노드들도 모두 방문처리되었다는 사실을 알게되었으므로 회색처리한다.

Step 5

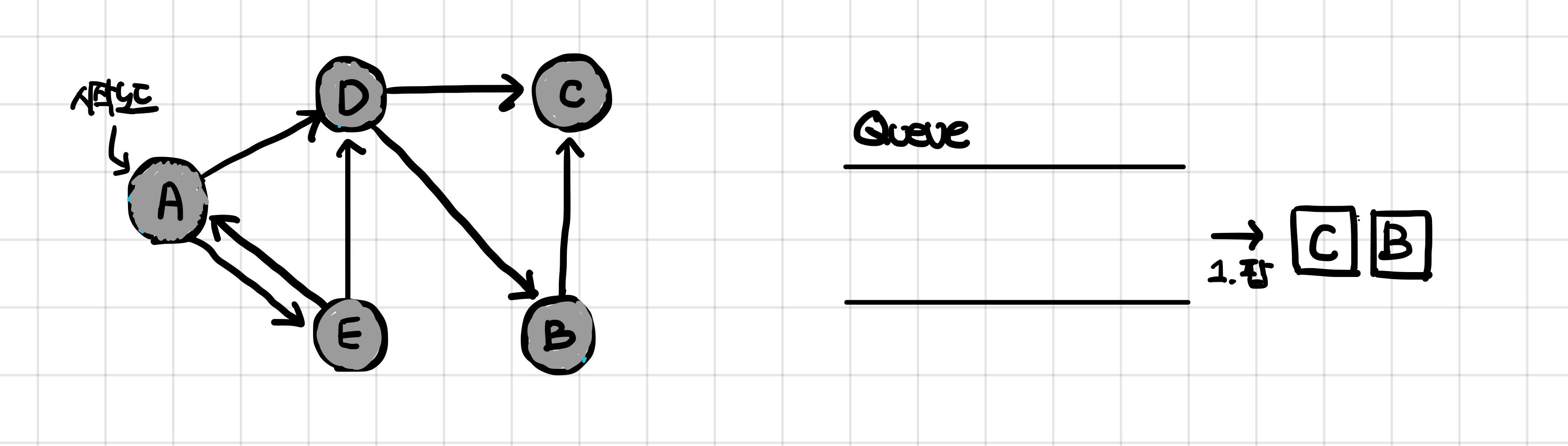
큐에 남아있던 B와 C 노드는 가장자리에 있던 순서대로 순차적으로 팝해주면서 각각 인접 노드를 확인한다.

B 노드는 인접노드인 C 노드가 방문처리되었기 때문에, 그리고 C 노드는 인접노드가 아예 없으므로 둘 다 회색으로 처리해주고, 아무 행동 하지 않는다.

큐에 더 이상 남아있는 노드가 없게 되었으므로 더 이상 탐색을 할 것이 없다고 판단하여 과정은 종료된다.

최종 순서

A -> D -> E -> B -> C

BFS를 Queue를 사용해서 구현해보기 [파이썬]

N = 5 # node수
V = 1 # 시작노드

# 자기 자신과는 False, Index 0은 모두 False
graph = [
  [False, False, False, False, False, False], # index 0을 사용하지 않음
  [False, False, False, False, True, True], # 1: {4, 5}
  [False, False, False, True, False, False], # 2: {3}
  [False, False, False, False, False, False], # 3: {}
  [False, False, True, True, False, False], # 4: {2, 3}
  [False, True, False, False, True, False], # 5: {1, 4}
]

# 설정된 그래프에서 방문한 곳을 True로 설정
visited = [False] * (N + 1)

def bfs(V) :
  # List 보다 pop 메서드의 시간복잡도가 더 낮은 deque 구조 사용
  q = deque([V]) # 시작노드를 넣은 상태에서 Queue 시작
  visited[V] = True # 시작노드 방문 처리
  while q : # Queue에 노드가 들어있다면 계속 반복
    V = q.popleft() # Queue의 가장자리에 있는 값
    print(V, end=' ')
    for i in range(1, N+1) : # index 0은 패스 (graph 그려줄 때부터 0은 패스함)
      # 인접노드가 아직 방문하지 않았고, 팝한 노드와 인접한 노드인지 확인
      if not visited[i] and graph[V][i] : 
        q.append(i) # Queue에 추가
        visited[i] = True # 방문처리
      
bfs(V)

from collections import defaultdict, deque

graph = [
  (1, 2),
  (1, 3),
  (2, 4),
  (2, 5),
  (3, 6),
  (3, 7),
  (4, 8),
  (5, 8),
  (6, 9),
  (7, 9),
]

start = 1

# 그래프를 인접리스트로 변환한다
adjacent_list = defaultdict(list)
for u, v in graph :
  adjacent_list[u].append(v)

# BFS 탐색 함수
def bfs(start, visited, result) :
  
  #* 탐색 시 최초 방문 노드 푸시하고 방문 처리
  queue = deque([start])
  visited.add(start)
  result.append(start)
  
  # 큐가 차있는 동안은 계속 반복
  while queue :
    node = queue.popleft() #* 큐 안에 있는 원소들 중 가장 먼저 푸시되었던 원소 팝
    for neighbor in adjacent_list.get(node, []) : # 현재 노드와 인접한 노드들
      if neighbor not in visited : # 아직 방문하지 않은 노드라면
        #* 인접 노드 방문 처리
        queue.append(neighbor)
        visited.add(neighbor)
        result.append(neighbor)
  
visited = set() # 방문한 노드를 저장할 set
result = []

bfs(start, visited, result)
print(result)

코드에 대한 설명은 주석으로 충분할 것 같다. 한 줄 한 줄 씩 차근차근 읽으면서 위의 흐름에 대입해서 생각하다보면 코드도 이해가 될 거라고 생각한다.

깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 비교

이렇게 DFS와 BFS를 모두 한 번 이해해보았다. 이 두 알고리즘들은 크게 보기에는 둘 다 그래프를 탐색하는 알고리즘이기 때문에 별 차이 없는 거 아니야? 그냥 방식만 조금 다른거 아니야? 취향 차이 아니야? 이렇게 느끼기 쉽지만 두 알고리즘이 활용하는 영역에서의 차이는 분명히 있다는 걸 기억해야 한다.

DFS는 그래프에서 깊게 들어가면서 탐색을 진행하고 더 이상 깊게 들어갈 곳이 없을 때 다시 되돌아오는 특성의 탐색 방식이고,

BFS는 가중치가 없는 그래프에서 최단 경로로 목표 노드를 향해 간다는 것을 보장한다.

📌 왜 너비 우선 탐색(BFS)는 최단 경로를 보장하는 걸까?

→ BFS의 알고리즘이 시작 노드로부터 도달 가능한 모든 노드들을 "거리"(즉, 시작 지점으로부터의 단계 수)에 따라 순차적으로 탐색하기 때문이다. 나는 그냥 처음에 이해할 때 생각보다 잘 이해가 안되서 시작 노드를 "나"라고 생각했을 때 아무래도 나랑 제일 가까이 있는 거부터 탐색한다는 소리는 내가 가고자 하는 목적지를 향해 꼬불꼬불 먼 길을 통해서 일부러 가지 않는다는 걸 의미한다고 생각했다.

DFS를 어디에 활용할 수 있는데?

DFS는 가장 깊은 곳으로 파고 들어가면서 탐색하고, 더 이상 탐색할 곳이 없을 시에 백트래킹하여 다시 최근 방문 노드로 돌아와서 다시 같은 방법으로 탐색을 진행한다는 특징을 가지고 있다.

따라서, 모든 가능한 해를 찾는 백트레킹 알고리즘 구현, 혹은 그래프 사이클 감지 등의 케이스에서 활용할 수 있다.

📌 코딩 테스트 TIP

그래프 탐색과 관련된 문제가 나왔을 때, 최단 경로를 찾는 문제가 아니면 무조건 DFS를 우선적으로 고려해보자!

BFS는 어디에 활용할 수 있는데?

BFS는 앞에서 말했다시피 찾은 노드가 시작 노드로부터 최단 경로임을 보장하는 탐색 방식이다.

따라서, 문제에 대해서 여러가지 다양한 답이 있을 경우에 가장 가까운 최단 경로의 답을 찾을 때 유용하다.

(최단 경로 찾기, 네트워크 분석 문제)

마무리하며

DFS, BFS는 코딩 테스트 단골 문제이면서 두 유형은 항상 자주 결합해서 구분지어서 사용해야 하는 경우가 많기 때문에 각각의 탐색 방식들의 특징을 기억하고 잘 활용할 수 있어야 할 것이다.

저작자표시 비영리 변경금지

들어가기

너비 우선 탐색 (BFS)

BFS 과정 순차적으로 정리하기

BFS 핵심 알아보기

BFS의 과정을 세부적으로 따라가보자

BFS를 Queue를 사용해서 구현해보기 [파이썬]

깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 비교

DFS를 어디에 활용할 수 있는데?

BFS는 어디에 활용할 수 있는데?

마무리하며

티스토리툴바